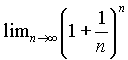 a vztahu
a vztahu
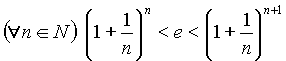
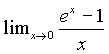 a
a
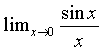 .
.
OKRUHY KE ZKOUŠCE Z MATEMATICKÉ ANALÝZY
1. roč., 1. sem. ZS2
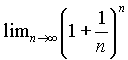 a vztahu
a vztahu
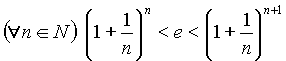
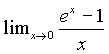 a
a
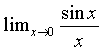 .
.
OKRUHY KE ZKOUŠCE Z MATEMATICKÉ ANALÝZY
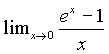 a
a
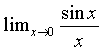 .
.
OKRUHY KE ZKOUŠCE Z MATEMATICKÉ ANALÝZY
2. roč., 3. sem. ZS2
OKRUHY KE ZKOUŠCE Z MATEMATICKÉ ANALÝZY
2. roč., 4. sem. ZS2