Parciální derivace vyšších řádů

import math 
from sympy import *
x, y, z, s, t = symbols('x y z s t')

f = x * sin(x**2 + 5 * x *y)
# Def. obor této funkce je R_2
f_x  = diff(f, x)
f_y = diff(f, y)
display(f_x) 
display(f_y)

$\displaystyle x \left(2 x + 5 y\right) \cos{\left(x^{2} + 5 x y \right)} + \sin{\left(x^{2} + 5 x y \right)}$

$\displaystyle 5 x^{2} \cos{\left(x^{2} + 5 x y \right)}$

# Spočtěme derivace druhého řádu:
f_xy = diff(f_y, x)
f_yx =  diff(f_x, y)
print(f_xy == f_yx)
display(f_xy)
display(f_yx)

True

$\displaystyle - 5 x^{2} \left(2 x + 5 y\right) \sin{\left(x^{2} + 5 x y \right)} + 10 x \cos{\left(x^{2} + 5 x y \right)}$

$\displaystyle - 5 x^{2} \left(2 x + 5 y\right) \sin{\left(x^{2} + 5 x y \right)} + 10 x \cos{\left(x^{2} + 5 x y \right)}$

# derivace druheho řádu
# zadejme předpis funkce
f = 2 * x**2 - y**2 + x * y  # funkce dvou proměnných
# vypočtěme nejdříve parc. derivace prvního řádu v obecném bodě:
f_x = diff(f, x) ; f_y  = diff(f, y)
f_x , f_y

(4*x + y, x - 2*y)

D_f = derive_by_array(f, [x, y])
print("gradient f  = ",D_f)

gradient f  =  [4*x + y, x - 2*y]

# spočtěme derivace druhého řádu v obecném bodě:
D2_f = derive_by_array(D_f, [x, y])
D2_f

[[4, 1], [1, -2]]

$$ D'' _f = \left[\begin{matrix}4 & 1\\1 & -2\end{matrix}\right] = \textrm{ Hessova matice} $$

Taylorův polynom funkce jedné proměnné

from sympy import *
x, y = symbols('x y')
series(sin(x), x, n = 10)

x - x**3/6 + x**5/120 - x**7/5040 + x**9/362880 + O(x**10)

series(exp(-x**2), x, x0 = 1, n = 3)

exp(-1) - 2*(x - 1)*exp(-1) + (x - 1)**2*exp(-1) + O((x - 1)**3, (x, 1))

Pro více informací viz. následující stránka na Wikipedii.

Taylorův rozvoj - více proměnných

Příklad: Taylorův polynom 1. stupně

######### Zde je hlavička ################
import sympy as sym 
from sympy.plotting import plot3d
from IPython.display import Math, display, Latex
import numpy as np
sym.init_printing()

########## Definice funkce ################
x, y = sym.symbols('x y')
f = (x**4) * (y**2) - x * y
display(Math("f(x,y)= %s" %sym.latex(f)))
pokracovat = input("Pro pokračování stiskni enter")
###########################################

########## Výpočty parc. derivací v obecném bodě ########################
display(Math("\\text{ Vypočítejme parciální\
             derivaci v obecném bodě } \\frac{\partial f}{\partial x}: "))
f_x = sym.diff(f, x)
pokracovat = input("Pro výsledek stiskni enter")
display(Math("\\frac{\partial f}{\partial x} = %s" %sym.latex(f_x)))

display(Math("\\text{ Vypočítejme parciální\
             derivaci v obecném bodě } \\frac{\partial f}{\partial y}: "))
pokracovat = input("Pro výsledek stiskni enter")
f_y = sym.diff(f, y)
display(Math("\\frac{\partial f}{\partial y} = %s" %sym.latex(f_y)))
pokracovat = input("Pro pokračování stiskni enter")
###########################################################################

############# Střed polynomu a parc. derivace ve středu polynomu ##########
a = float(input("Zadejte 1. souřadnici středu polynomu: a =  "))
b = float(input("Zadejte 2. souřadnici středu polynomu: b =  "))
display(Math("\\text{Spočítejte funkční hodnotu funkce } f(%g,%g):" %(a,b)))
pokracovat = input("Pro výsledek stiskni enter")
display(Math("f(%g,%g) = %g" %(a,b, f.subs({x: a, y: b}))))
display(Math("\\text{Spočítejte hodnotu } \\frac{\partial f}{\partial x}\
               (%g,%g): " %(a,b)))
pokracovat = input("Pro výsledek stiskni enter")
display(Math("\\frac{\partial f}{\partial x}(%g,%g)\
               = %g" %(a,b,f_x.subs({x: a, y: b}))))
display(Math("\\text{Spočítejte hodnotu } \\frac{\partial f}{\partial y}\
               (%g,%g): " %(a,b)))
pokracovat = input("Pro výsledek stiskni enter")
display(Math("\\frac{\partial f}{\partial y}(%g,%g)\
               = %g" %(a,b,f_y.subs({x: a, y: b}))))

###########################################################################

############### Taylorův polynom se středem (a,b) 1. stupně ###############
display(Math("\\text{Napište předpis Taylorova polynomu se středem v bodě } \
        S = (%g,%g),\\quad T_{1,f,S}(x,y):" %(a,b)))
pokracovat = input("Pro výsledek stiskni enter")
T_f = f.subs({x: a, y: b}) +\
         f_x.subs({x: a, y: b}) * (x - a) + f_y.subs({x: a, y: b}) * (y - b)
display(Math("T_{1,f,S}(x,y) = %s " %sym.latex(T_f)))

###########################################################################

###################### Graf funkce f(x,y) a polynomu T(x,y) ###############
# to set features of the plot, turn the plotting off, then make adjustments, then show the plot

# create a plot object
p = sym.plotting.plot3d(T_f,show=False)

# change the y-axis of the entire plot
# p.xlim = (0,50)

# change a feature of only the first plot object (the line, in this case there is only one)
p[0].line_color = 'm'
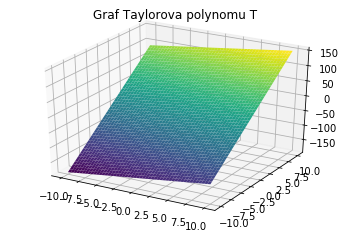
p.title = 'Graf Taylorova polynomu T'

# now show the line
p.show()



###########################################################################

$\displaystyle f(x,y)= x^{4} y^{2} - x y$

Pro pokračování stiskni enter

$\displaystyle \text{ Vypočítejme parciální derivaci v obecném bodě } \frac{\partial f}{\partial x}: $

Pro výsledek stiskni enter

$\displaystyle \frac{\partial f}{\partial x} = 4 x^{3} y^{2} - y$

$\displaystyle \text{ Vypočítejme parciální derivaci v obecném bodě } \frac{\partial f}{\partial y}: $

Pro výsledek stiskni enter

$\displaystyle \frac{\partial f}{\partial y} = 2 x^{4} y - x$

Pro pokračování stiskni enter
Zadejte 1. souřadnici středu polynomu: a =  1
Zadejte 2. souřadnici středu polynomu: b =  2

$\displaystyle \text{Spočítejte funkční hodnotu funkce } f(1,2):$

Pro výsledek stiskni enter

$\displaystyle f(1,2) = 2$

$\displaystyle \text{Spočítejte hodnotu } \frac{\partial f}{\partial x} (1,2): $

Pro výsledek stiskni enter

$\displaystyle \frac{\partial f}{\partial x}(1,2) = 14$

$\displaystyle \text{Spočítejte hodnotu } \frac{\partial f}{\partial y} (1,2): $

Pro výsledek stiskni enter

$\displaystyle \frac{\partial f}{\partial y}(1,2) = 3$

$\displaystyle \text{Napište předpis Taylorova polynomu se středem v bodě } S = (1,2),\quad T_{1,f,S}(x,y):$

Pro výsledek stiskni enter

$\displaystyle T_{1,f,S}(x,y) = 14.0 x + 3.0 y - 18.0 $

Příklad

Uvažujme funkci $f(x_1,x_2)=x_1^2x_2. $ Nyní spočítejme Taylorův polynom nejvýše třetího stupně se středem v bodě $(0,0).$

Řešení

Zde zadefinujme předpis funkce $f.$

######### Zde je hlavička ################
import sympy as sym 
from IPython.display import Math, display, Latex, HTML
import numpy as np
sym.init_printing()
###########################################

############ Definice funkce #############################
h1, h2, x1, x2, t = sym.symbols('h1 h2 x1 x2 t')
f = x1**2 * x2
display(Math("\\text{Předpis zadané funkce je: } f(x_1,x_2) = %s"\
            %sym.latex(f)))
a = float(input("Zadej první souřadnici středu T. polynomu: "))
b = float(input("Zadej druhou souřadnici středu T. polynomu: "))
pokracovat = input("Pro pokračování stiskni enter ")
###########################################################

######## Průřezová funkce - předpis v obecném bodě  #######
display(Math("\\text{ Dále najděte\
             předpis průřezové funkce } g(t) =f(x+th):"))
print()
pokracovat = input("Pro pokračování stiskni enter: ")
x = np.array([x1, x2])
h = np.array([h1, h2]) 
g = f.subs({x1: (x + t * h)[0], x2: (x + t * h)[1]})
g_subs = g.subs({x1: a, x2: b})
display(Math("g(t) = %s = %s" %(sym.latex(g_subs), sym.latex(g_subs.expand()))))
print("***************************************")
###########################################################

########## g(0), g'(0), g''(0), g'''(0) #####################
g0 = g_subs.subs(t, 0)
Dg0 = sym.diff(g_subs, t, 1).subs(t, 0)
D2g0 = sym.diff(g_subs, t, 2).subs(t, 0)
D3g0 = sym.diff(g_subs, t, 3).subs(t, 0)
display(Math("\\text{ Najděte } g(0) = ?"))
pokracovat = input("Pro výsledek stiskněme enter ")
display(Math("g(0) = %g" %g0))
print("***************************************")
display(Math("\\text{ Najděte } g'(0) = ? "))
pokracovat = input("Pro pokračování stiskněte enter ")
display(Math("g'(0) = %s" %sym.latex(Dg0)))
print("****************************************")
display(Math("\\text{ Najděte } g''(0) = ? "))
pokracovat = input("Pro pokračování stiskněte enter ")
display(Math("g''(0) = %s" %sym.latex(D2g0)))
print("****************************************")
display(Math("\\text{ Najděte } g'''(0) = ? "))
pokracovat = input("Pro pokračování stiskněte enter ")
display(Math("g'''(0) = %s" %sym.latex(D3g0)))
print("****************************************")
###########################################################

######### Taylorův polynom T(h1, h2) = ####################
display(Math("\\text{ Najděte předpis Taylorova polynomu \
        nejvýš 3. stupně } T(h_1, h_2) = "))
pokracovat = input("Pro pokračování stiskněte enter ")
T = g0 + Dg0 + D2g0/2 + D3g0/6
T.expand()
display(Math("T_{f, (%g,%g), 3}(h_1,h_2) = %s"\
            %(a, b, sym.latex(T))))

$\displaystyle \text{Předpis zadané funkce je: } f(x_1,x_2) = x_{1}^{2} x_{2}$

Zadej první souřadnici středu T. polynomu: 0
Zadej druhou souřadnici středu T. polynomu: 0
Pro pokračování stiskni enter 

$\displaystyle \text{ Dále najděte předpis průřezové funkce } g(t) =f(x+th):$

Pro pokračování stiskni enter: 

$\displaystyle g(t) = h_{1}^{2} h_{2} t^{3} = h_{1}^{2} h_{2} t^{3}$

***************************************

$\displaystyle \text{ Najděte } g(0) = ?$

Pro výsledek stiskněme enter 

$\displaystyle g(0) = 0$

***************************************

$\displaystyle \text{ Najděte } g'(0) = ? $

Pro pokračování stiskněte enter 

$\displaystyle g'(0) = 0$

****************************************

$\displaystyle \text{ Najděte } g''(0) = ? $

Pro pokračování stiskněte enter 

$\displaystyle g''(0) = 0$

****************************************

$\displaystyle \text{ Najděte } g'''(0) = ? $

Pro pokračování stiskněte enter 

$\displaystyle g'''(0) = 6 h_{1}^{2} h_{2}$

****************************************

$\displaystyle \text{ Najděte předpis Taylorova polynomu nejvýš 3. stupně } T(h_1, h_2) = $

Pro pokračování stiskněte enter 

$\displaystyle T_{f, (0,0), 3}(h_1,h_2) = h_{1}^{2} h_{2}$

Smíšené derivace a jejich rovnost

Mějme dánu funkci předpisem: $$ f(x,y)= \begin{cases} xy\frac{x^2-y^2}{x^2+y^2}, &\text{jestliže $x^2+y^2\neq 0$;}\\ 0, &\text{jestliže $x^2+y^2=0$.} \end{cases} $$ Dokažte, že potom platí: $$ \frac{\partial^2f}{\partial x\partial y}(0,0)=1\neq -1=\frac{\partial^2f}{\partial y\partial x}(0,0). $$

from sympy import *
x, y, z = symbols('x y z')
def f(x, y):
    if x**2 + y**2 != 0:
        z = x * y * (x**2 - y**2)/(x**2 + y**2)
    else:
        z = 0
    return z
print(diff(f(x,y), x, y) - diff(f(x,y), y, x))
# Spočtěme parc. derivace prvního řádu v počátku:
f_x_00 = limit((f(x, 0)- f(0,0)/x), x, 0)
f_y_00 = limit((f(0, y) - f(0, 0)/y), y, 0)
def f_x(a, b):
    if x**2 + y**2 != 0:
        z = diff(f(x,y), x).subs({x: a,y: b})
    else:
        z = f_x_00
    return z 
def f_y(a, b):
    if x**2 + y**2 != 0:
        z = diff(f(x,y), y).subs({x: a,y: b})
    else:
        z = f_y_00
    return z 
print("f_x(0,y) = ", f_x(0,y))
print("f_x(0,0) = ", f_x(0,0))
f_xy_00 = limit((f_x(0,y) - f_x(0,0))/y, y, 0)
f_yx_00 = limit((f_y(x,0) - f_y(0,0))/x, x, 0)
print("f_xy(0,0) = ",f_xy_00,", f_yx(0,0) = ", f_yx_00)
        

0
f_x(0,y) =  -y
f_x(0,0) =  0
f_xy(0,0) =  -1 , f_yx(0,0) =  1

# Upravme kód, aby jsme mohli na vstupu z konzole 
# mohli vložit předpis funkce
from sympy import *
from sympy.plotting import  plot3d 
x, y, z = symbols('x y z')
A = float(input("Zadejme souřadnici A bodu P = (A,B): "))
B = float(input("Zadejme souřadnici B bodu P = (A,B): "))
print(f"P = ({A},{B}).")
expr1 = S(input("Zadej předpis funkce mimo bod P = (A,B):\n\
          f(x,y) = "))
C = float(input(f"Zadejme hodnotu funkce f v bodě P: \n\
           f(P) = f({A},{B}) =  "))
# expr1 = S(input("Zadej předpis funkce mimo bod P = (A,B): ")
#)
# expr1 = x * y * (x**2 - y**2)/(x**2 + y**2)
# A = 0
# B = 0
# C = 0
def f(a, b):
    if (a - A)**2 + (b - B)**2 != 0:
        z = expr1.subs({x: a,y: b})
    else:
        z = C
    return z
f_x_P = limit((f(A + x, B)- f(A,B)/x), x, 0)
f_y_P = limit((f(A, B + y) - f(A, B)/y), y, 0)
def f_x(a, b):
    if (a - A)**2 + (b - B)**2 != 0:
        z = diff(f(x,y), x).subs({x: a,y: b})
    else:
        z = f_x_P
    return z 
def f_y(a, b):
    if (a - A)**2 + (b - B)**2 != 0:
        z = diff(f(x,y), y).subs({x: a,y: b})
    else:
        z = f_y_P
    return z 
print(f"f_x({A},{B}) = ", f_x_P)
print(f"f_y({A},{B}) = ", f_y_P)
f_xy_P = limit((f_x(A,B + y) - f_x(A,B))/y, y, 0)
f_yx_P = limit((f_y(A + x,B) - f_y(A,B))/x, x, 0)
print(f"f_xy({A},{B}) = ",f_xy_P,f", f_yx({A},{B}) = ", f_yx_P)
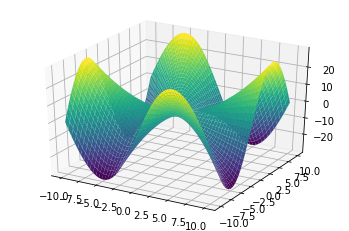
plot3d(f(x,y))

Zadejme souřadnici A bodu P = (A,B): 0
Zadejme souřadnici B bodu P = (A,B): 0
P = (0.0,0.0).
Zadej předpis funkce mimo bod P = (A,B):
          f(x,y) = x * y * (x**2 - y**2)/(x**2 + y**2)
Zadejme hodnotu funkce f v bodě P: 
           f(P) = f(0.0,0.0) =  0
f_x(0.0,0.0) =  0
f_y(0.0,0.0) =  0
f_xy(0.0,0.0) =  -1 , f_yx(0.0,0.0) =  1

<sympy.plotting.plot.Plot at 0x104c7f6d8>