Střední hodnota náhodné veličiny

Definice střední hodnoty

Definice Nechť $X$ je náhodná veličina. Střední hodnotou náhodné veličiny $X$ budeme nazývat číslo $EX$, definované vztahem: $$ EX = \sum_i x_ip_(x_i) \ \ \ \ \text{pro diskrétní n.v.} $$ $$ EX = \int_{-\infty}^{\infty} xf(x)dx \ \ \ \text{pro spojitou náhodnou n.v.} $$ Rozptylem (disperzí) náhodné veličiny $X$ rozumíme číslo: $$ DX = E[(X-EX)^2]. $$

Vlastnosti střední hodnoty

Věta.

(a) Nechť $k$ je konstanta a $X = k$, potom $$ EX = Ek = k,\ \ \ E(kX) = k\cdot EX. $$ (b) Jsou-li $X,Y$ dvě náhodné veličiny, pak platí: $$ E(X+Y) = EX + EY. $$ (c) Nechť $X_1,\ldots,X_n$ jsou náhodné veličiny. Potom platí: $$ E(X_1 + X_2 +\ldots + X_n) = EX_1 + EX_2 +\ldots + EX_n. $$ (d) Nechť $X_1,\ldots,X_n$ je libovolná n-tice nahodných veličin, nechť $k_1,k_2,\ldots,k_n,b$ jsou libovolné konstanty a $n\in\mathbb N.$ Potom platí: $$ E(\sum_{i=1}^n k_i X_i + b) = \sum_{i=1}^n k_i EX_i + b. $$ (e) Jsou-li $Y,Y$ dvě nezávislé náhodné veličiny, pak platí: $$ E(XY) = EX\cdot EY. $$ Jsou-li $X_1,\ldots,X_n$ nezávislé náhodné veličiny a $n\in\mathbb N,$ potom platí: $$ E(\prod_{i=1}^n X_i) = \prod_{i=1}^n EX_i. $$

Příklad

In [15]:
from IPython.display import HTML, display, Math, Latex

Náhodná veličina $X$ je tabulkou rozdělení pravděpodobností. Určete střední hodnotu náhodné veličiny $X$ a náhodné veličiny $Y$ definované vztahem $Y = 4X^2 - 1.$

$x_i$ 0 2 4 6
$p(x_i)$ 0.2 0.3 0.4 0.1

Řešení

In [30]:
import numpy as np
x = np.array([0, 2, 4, 6])
p = np.array([0.2, 0.3, 0.4, 0.1])
EX = np.dot(x, p)
display(Math("EX = \\sum_{i=1}^{%g} x_ip(x_i) =  %g" %(len(x),EX)))
$\displaystyle EX = \sum_{i=1}^{4} x_ip(x_i) = 2.8$

K výpočtu střední hodnoty n.v. $Y$ využijeme vlastnost (7) z Věty 1. Pak totiž máme: $$ EY = E(4X^2 -1)= 4EX^2 -E1 = 4EX^2 - 1. $$

In [31]:
E = np.dot(x**2, p)
display(Math("EX^2 = \\sum_{i=1}^{%g}\
        x_i^2\\cdot p(x_i) =  %g" %(len(x),E)))
print("A dále pokračujeme ve výpočtu: ")
EY = 4 * E - 1
display(Math("EY = 4EX^2 - 1 = 4\\cdot %g - 1= %g" %(E, EY)))
$\displaystyle EX^2 = \sum_{i=1}^{4} x_i^2\cdot p(x_i) = 11.2$ 
A dále pokračujeme ve výpočtu:
$\displaystyle EY = 4EX^2 - 1 = 4\cdot 11.2 - 1= 43.8$

Příklad

Při hře Člověče, nezlob se může hráč nasadit první figuru na hrací pole až tehdy, když mu padne na hrací kostce šestka. Definujme náhodnou veličinu tak, aby vyjadřovala počet provedených hodů do zahájení hry a vypočítejte střední hodnotu této náhodné veličiny.

Řešení

Náhodná veličina $X$ nabývá hodnot $1,2,3,\ldots$ Nejdříve vypočítáme pravděpodobnosti pro jednotlivé hodnoty: $P(\{X=k\}) = (5/6)^{k-1}\cdot (1/6), k = 1, 2, 3,\ldots$ $$ EX = \sum_{i=1}^{\infty} x_ip(x_i) $$

In [47]:
######### Zde je hlavička ################
import sympy as sym 
from sympy.plotting import plot3d
from IPython.display import Math, display, Latex
import numpy as np
sym.init_printing()
# Numericky sečteme částečnou sumu (12)
def s(n):
    x = np.array([i for i in range(n)])
    p = np.array([(5/6)**(i - 1) * (1/6) for i in range(n)])
    EX = np.dot(x, p)
    return EX
s(50)
Out[47]:
$\displaystyle 5.9927476019382695$
In [65]:
x_i = i
p_i = sym.Rational(5,6)**(i - 1) * sym.Rational(1,6)
suma = sym.Sum(x_i * p_i, (i, 1, n))
display(Math("\\text{Častečný součet je roven sumě: }\
              s_n = \\sum_{i=1}^n\
             x_ip(x_i) = %s" %sym.latex(suma)))
sn = suma.doit()
display(Math("s_n = %s  = %s"\
             %(sym.latex(suma), sym.latex(suma.doit().simplify()))))
EX = sym.limit_seq(sn)
display(Math("EX = \\lim_{n\\to\infty}\
              (%s) = %s." %(sym.latex(suma), EX)))
$\displaystyle \text{Častečný součet je roven sumě: } s_n = \sum_{i=1}^n x_ip(x_i) = \sum_{i=1}^{n} \frac{\left(\frac{5}{6}\right)^{i - 1} i}{6}$
$\displaystyle s_n = \sum_{i=1}^{n} \frac{\left(\frac{5}{6}\right)^{i - 1} i}{6} = 6^{- n} \left(- 5^{n} n - 6 \cdot 5^{n} + 6^{n + 1}\right)$
$\displaystyle EX = \lim_{n\to\infty} (\sum_{i=1}^{n} \frac{\left(\frac{5}{6}\right)^{i - 1} i}{6}) = 6.$

Příklad

Vypočtěte disperzi(rozptyl) náhodné veličiny $X$ z předchozího příkladu. Disperzi spočítáme podle vzorce: $$ DX = EX^2 -(EX)^2. $$

Řešení

Spočítejme nejdříve střední hodnotu $EX^2.$

In [67]:
suma2 = sym.Sum(x_i**2 * p_i, (i, 1, n))
s_2n = suma2.doit()
display(suma2)
display(s_2n)
EX2 = sym.limit_seq(s_2n)
display(EX2)
display(Math("EX^2 = \\sum_{i=1}^{\infty}x_i^2p(x_i) = \
              \\lim_n(%s) = %s" %(sym.latex(suma2),EX2)))
$\displaystyle \sum_{i=1}^{n} \frac{\left(\frac{5}{6}\right)^{i - 1} i^{2}}{6}$
$\displaystyle - \left(\frac{5}{6}\right)^{n} n^{2} - 12 \left(\frac{5}{6}\right)^{n} n - 66 \left(\frac{5}{6}\right)^{n} + 66$
$\displaystyle 66$
$\displaystyle EX^2 = \sum_{i=1}^{\infty}x_i^2p(x_i) = \lim_n(\sum_{i=1}^{n} \frac{\left(\frac{5}{6}\right)^{i - 1} i^{2}}{6}) = 66$

Nyní dosaďme do vzorce (13):

In [68]:
DX = EX2 - (EX)**2
display(Math("DX = EX^2 -(EX)^2 = %g - (%g)^2 = \
              %g." %(EX2, EX, DX)))
$\displaystyle DX = EX^2 -(EX)^2 = 66 - (6)^2 = 30.$

Příklad

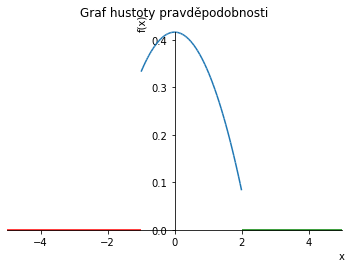
Uvažujme náhodnou veličinu $X$, která má hustotu pravděpodobnosti danou předpisem:

[ f(x)= \begin{cases} \frac{-1}{12}(x^2 -5),\ \ \ x\in\langle -1,2\rangle\\ 0,\ \ \ x\notin\langle -1,2\rangle. \end{cases} ] (a) Nakreslete graf hustoty pravděpodobnosti a distribuční funkce.

(b) Spočítejme střední hodnotu n.v. X.

(c) Spočítejme modus a medián n.v. $X.$

Řešení

In [70]:
x = sym.symbols('x')
y1 = 0
y2 = (-1/12) * (x**2 - 5)
y3 = 0
p = sym.plotting.plot(y2,(x,-1,2),show=False )
# p[0].label = '$%s$'%y
p.extend( sym.plotting.plot(y1,(x,-5,-1),show=False ) )
p[1].line_color = "r"
p.extend( sym.plotting.plot(y3,(x,2,5),show=False ) )
p[2].line_color = "g"
# p.legend = True
p.title = "Graf hustoty pravděpodobnosti"
p.show()

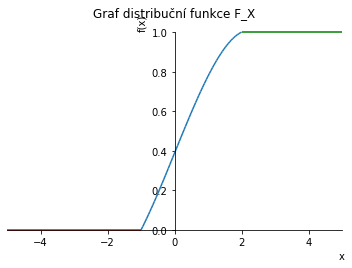
Nyní hledejme přepis distribuční funkce $F_X$ n.v. X. Zjistíme, že $$ F_X(x) = \begin{cases} 0, \ \ \ x\in (-\infty,-1\rangle\\ \frac{-1}{36}(x^3-15x-14),\ \ \ x\in(-1,2\rangle\\ 1, \ \ \ x\in(2,\infty). \end{cases} $$ Zde jak víme platí: $$ F_X(x) = \int_{-\infty}^x f(t)dt $$ a skoro všude platí, že $F_X'(x) = f(x).$

In [71]:
x = sym.symbols('x')
y1 = 0
y2 = (-1/36) * (x**3 - 15 * x -14)
y3 = 1
p = sym.plotting.plot(y2,(x,-1,2),show=False )
# p[0].label = '$%s$'%y
p.extend( sym.plotting.plot(y1,(x,-5,-1),show=False ) )
p[1].line_color = "r"
p.extend( sym.plotting.plot(y3,(x,2,5),show=False ) )
p[2].line_color = "g"
# p.legend = True
p.title = "Graf distribuční funkce F_X"
p.show()

(b) Spočítejme střední hodnotu n.v. X.

$$ EX = \int_{-\infty}^{\infty} x\cdot f(x)dx = \int_{-\infty}^{-1}x\cdot 0dx + \int_{-1}^2 x\cdot\frac{-1}{12}(x^2-5)dx + \int_2^{\infty} x\cdot 0dx $$
In [72]:
EX = 0 + sym.integrate(x * (-1/12) * (x**2 - 5), (x, -1, 2)) + 0
display(Math("EX  = 0 + \int_{-1}^2 x\\cdot\\frac{-1}{12}(x^2-5)dx\
                + 0 = %g." %EX))
$\displaystyle EX = 0 + \int_{-1}^2 x\cdot\frac{-1}{12}(x^2-5)dx + 0 = 0.3125.$

(c) Spočítejme nyní modus a medián n.v. $X.$ Pro spojitou n.v. $X$ definujeme medián jako číslo $m_e$ splňující podmínku: \begin{equation}\label{eq: median} F_X(x) = 0.5 \end{equation}

Řešme proto rovnici:

In [23]:
from sympy import *
x = symbols('x') 
eq = Eq(S(-1/36) * (x**3 - 15 * x - 14), S(1/2))
display(eq)
solve(eq, domain = S.Reals )
$\displaystyle - 0.0277777777777778 x^{3} + 0.416666666666667 x + 0.388888888888889 = 0.5$
Out[23]:
[-4.00000000000000, 0.267949192431123, 3.73205080756888]

Mediánem je bod (m_e \approx 0.2679.)

Zbývá určit modus n.v. X. Hledejme maximum funkce (f_X(x)) na intervalu ((-1,2)).

Budeme derivovat funkci: (f_X(x)):

In [25]:
f_X = (-1/12) * (x**2 - 5)  
Df_X = diff(f_X, x)
display(Df_X)
$\displaystyle - 0.166666666666667 x$

Hledejme nulový bod 1. derivace v intervalu ((-1,2)).

In [28]:
nulBod = solve(Df_X)[0]
display(nulBod)
$\displaystyle 0.0$

Funkční hodnota hustoty pravděpodobnosti je (f_X(0) = 5/12.) Modus je roven číslu 0.

In [ ]: