Damped wave equation on graphs and asymptotics of eigenvalues

In the paper

P. Freitas, J. Lipovsky: Eigenvalue asymptotics for the damped wave equation on metric graphs, J. Diff. Eq. 263 (2017), 2780–2811

we considered the linear damped wave equation

∂tt wj(t,x) + 2aj(x) ∂t wj(t,x) = ∂xx wj(t,x) + bj(x) wj(t,x),

on a finite metric graph, where aj is the damping function and bj is the potential on the j-th edge. We found interesting results on the spectrum of the corresponding operator. The problem was previosly studied on a segment and on a manifold, but the metric graph provides an interesting intermediate case between a segment and a manifold.

We found that for an equilateral graph (a graph with the same lengths of the edges) sequences of eigenvalues are formed, with their real parts converging to a certain number as their imaginary parts going to infinity. These numbers we called high-frequency abscissas. We found upper and lower bounds on the number of high-frequency abscissas depending on the number of edges of an equilateral graph and its structure.

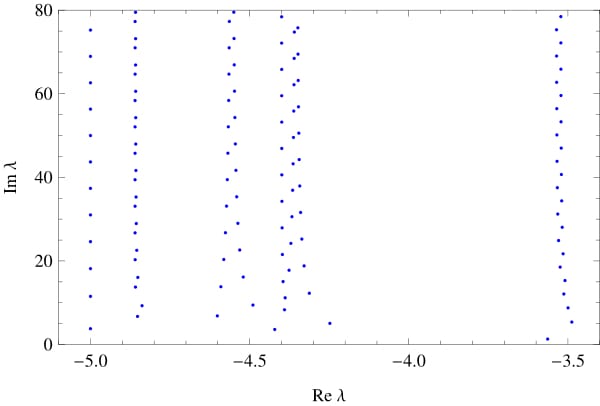
Figure 1: Spectrum of a certain equilateral graph with 5 edges.
Spectrum of a certain equilateral graph with 5 edges.

If the ratio of the lengths of the edges is irrational, the number of high-frequency abscissas can go to infinity.

Figure 2: Spectrum of a star graph with different lengths of the edges, l1 = 1, l2 = 1, l3 = 1.03.
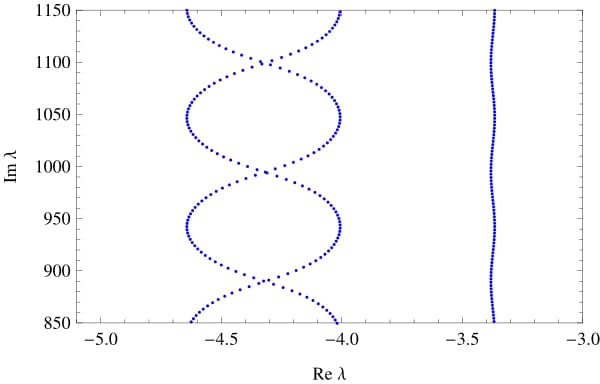
Spectrum of a star graph with different lengths of the edges, <i>l</i><sub>1</sub> = 1, <i>l</i><sub>2</sub> = 1, <i>l</i><sub>3</sub> = 1.03.
Figure 3: Spectrum of a star graph with different lengths of the edges, l1 = 1, l2 = 1, l3 = 1.41.
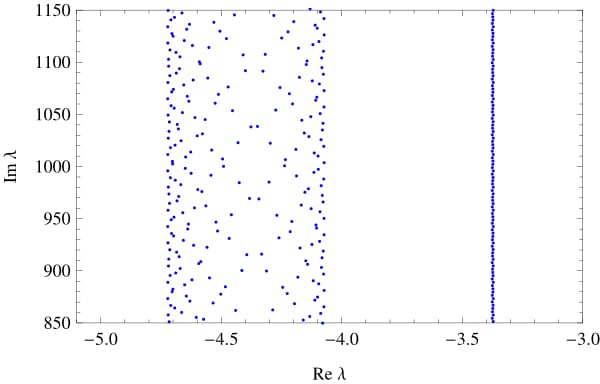
Spectrum of a star graph with different lengths of the edges, <i>l</i><sub>1</sub> = 1, <i>l</i><sub>2</sub> = 1, <i>l</i><sub>3</sub> = 1.41.