Diferenciální počet

Co je derivace funkce?

Derivace nám určuje velikost růstu či poklesu hodnoty funkce ku změně jejího argumentu.

Pojem derivace vznikl v 17. století v pracích Isaaca Newtona a Gottfrieda Wilhelma Leibnize při řešení fyzikálních problémů. Tyto fyzikální úlohy se zabývaly studiem síly a pohybu. Později vedly k formulaci Newtonových pohybových zákonů.

Historická definice derivace

Historické definice vyjadřovaly derivaci jako poměr růstu či poklesu zavislé proměné (nejčasteji značené jako y) ku změně nezávislé proměné (nejčasteji značené jako x) poté by se dala derivace zjednodušeně zapsat jako $\frac{Δ y}{Δ x}$ .

Derivace je hodnota $\frac{Δ y}{Δ x}$ , když se Δx blíží k nule. V takovém případě nahradíme znak Δ písmenem d. Vznikne nám poté zlomek $\frac{dy}{dx}$ , který naznačuje podíl dvou infinitezimálních hodnot (odborné označení pro nekonečně malé číslo, jehož hodnota je menší než jakékoliv kladné reálné číslo).

Moderní definice derivace

V průběhu vývoje matematiky se představa infinitezimálních hodnot ukázala jako nedostatečně přesná a byla nahrazena „ε-δ“ definicí limit. Moderní definice v bodě vypadá takto:

f ´ (x) = lim_{h \to 0} \frac{f (x + h) - f (x)}{h} = lim_{x \to a} \frac{f (x) - f (a)}{x - a} =

lim_{Δx \to 0} \frac{f (x+Δx) - f (x)}{Δx}

Zápis derivace

$f ´$
[f s čárkou]
$\frac{d}{dx} f (x)$
[d podle dx z fx]
$D_{x} f$
[D podle x z f]
$\overset{\cdot}{x} = \frac{dx}{dt} = x ´ (t)$
[Newtonova notace používa tečku nad proměnou používá se obvykle pouze ve fyzice pro derivování podle proměnne času (t)]

Geometrický význam derivace v bodě

Derivace nám určuje směrnici tečny v daném bodu funkce.

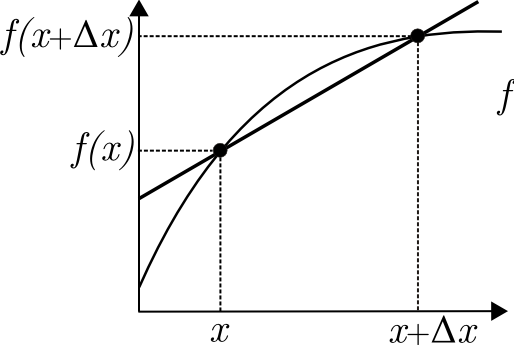
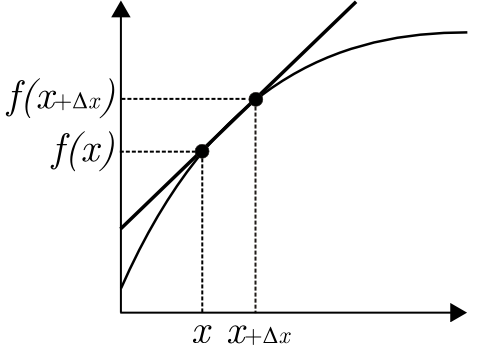
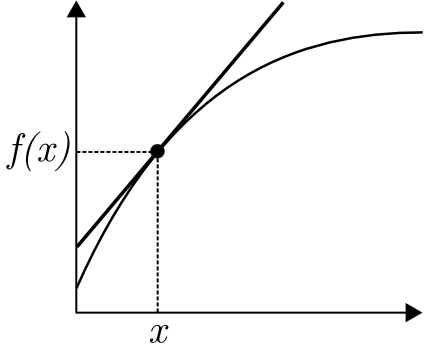
sečna křivky — $lim_{Δx \to 0} \frac{f (x+Δx) - f (x)}{Δx}$
Grafy znázorňující co se děje když se Δx→0 Grafy znázorňující co se děje když se Δx→0