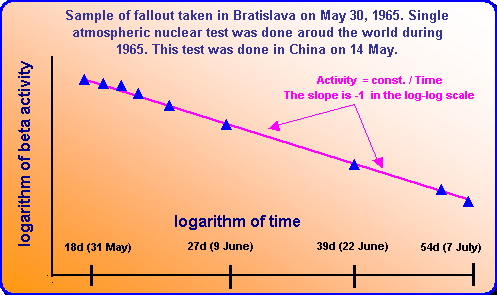
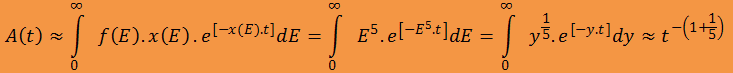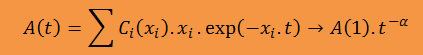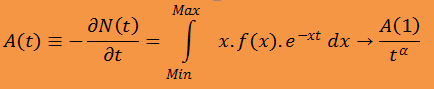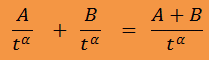POKLES CELKOVÉ RADIOAKTIVITY S ČASEM VE VELKÉ VZDÁLENOSTI OD JADERNÉHO VÝBUCHU NEBO NEHODY JADERNÉHO REAKTORU
Pokud je okamžik výbuchu nebo nehody použit jako počátek časové osy,
je celková radioaktivita ve velké vzdálenosti od zdroje nepřímoúměrná času.
Wayová a Wigner odvodili,
že pokud jsou uvažovány pouze události na úrovni jádra, potom celková radioaktivita neklesá s první mocninou času
(tedy nepřímoúměrně s časem), ale klesá s mocninou rovnou 1,2 = 6/5.
Podle jejich odvození je hodnota směrnice poklesu v log-log měřítku 1+1/5 důsledkem úměry
mezi rozpadovou konstantou a pátou mocninou rozpadové energie
(tento vztah mezi rozpadovou konstantou a rozpadovou energií byl zjištěn empiricky).
V odvození Way a Wignera bylo na štěpné produkty nahlíženo jako na statistický soubor;
odvození bylo provedeno pro beta rozpad za sekundu a pro celkovou uvolněnou energii v čase. Všechny vnější faktory jako například vzdálenost od výbuchu a meteorologické faktory byly zanedbány.
Dále předpokládali, že různé rozpadové energie jsou přibližně stejně časté
(f(E)=const, kde f(E) je četnost-hustota energie E).
Takto odvodili následující vztah:
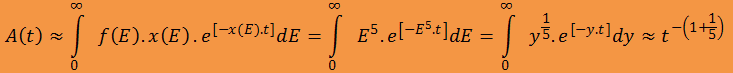
Tento model (pokles s mocninou 1,2) je příliš optimistický a nepopisuje reálná data
v případě časového poklesu ve velké vzdálenosti od centra výbuchu či nehody.
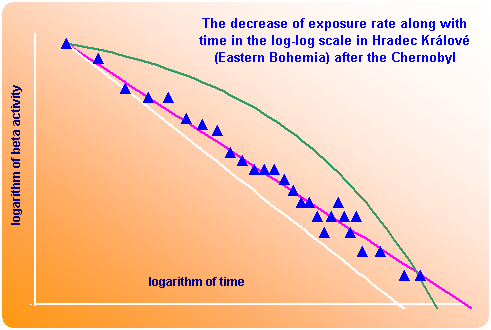Příklad poklesu fotonového dávkového příkonu s časem v log-log měřítku v
Hradci Králové po černobylské havárii ukazuje,
že pokud je okamžik havarie použit jako počátek časové osy, potom fotonový dávkový příkon klesá s první mocninou času.
Směrnice fialové přímky na obrázku je rovna přesně -1 a modrá přímka má směrnici přesně 1,2.
Obě tyto přímky jsou vytvořeny tak, že procházejí přesně maximální hodnotou.
Zelený oblouk na obrázku představuje hypotetický exponenciální pokles definovaný souřadnicemi maximální hodnoty
a první minimální hodnoty (zelený oblouk prochází přesně maximem a minimem-posledním bodem poklesu, takto by aktivita klesala pokud by byla přítomna pouze jedna rozpadová konstanta).
Obecně platí, že ve velké vzdálenosti od nehody nebo výbuchu, je celková radioaktivita součtem aktivit
několika nezávislých radionuklidů.
Jde tedy o sumu exponenciálních výrazů exp(-xi.t) s různými rozpadovými konstantami xi a s různým zastoupením v celkovém součtu
(každý exponenciální člen je násoben časově nezávislou konstantou Co(xi),
která představuje koncentraci konkrétního radionuklidu v čase t=0).
Platí:
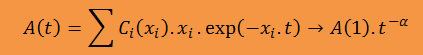
Platí, že pokles celkové aktivity je lineární a nikoli konkávní (zelený oblouk) v log-log měřítku.
Tato rovnice neplatí ve dvou následujících příkladech:
1) V případě přirozené radioaktivity je první rozpadový produkt v rovnováze s ostatními radionuklidy
(dceřiné radionuklidy) současně rozpadová konstanta x1 je velmi malá (doba života prvního členu radioaktivní řady je velká)
a celková radioaktivita je proto přibližně nezávislá na čase (zhlediska délky lidského života).
2) Druhý případ platí bezprostředně po jaderném výbuchu, kdy aktivita (a množství) jednotlivých radionuklidů se
navzájem ovlivňují i když nejsou příslušníky téže rozpadové řady
(parametery Co(xi) již nejsou konstanty a funkce f(x) nemůže být použita).
Pro tento případ Wayová a Wigner odvodili, že mocnina může být rovna 6/5.
Na rozdíl od situace bezprostředně po jaderném výbuchu lze popsat množstí radionuklidu
ve velké vzdálenosti od výbuchu exponenciálním výrazem a množství radionuklidu není ovlivněno ostatními radionuklidy.
Ve skutečnosti sice může nastat, že jsou přítomny rozpadové produkty, které jsou navzájem závislé,
ale taková podskupina muže být z hlediska celkové aktivity nahrazena jediným exponenciálním členem
(takové radionuklidy jsou ve vzájemné rovnováze, například pár 140Ba - 140La).
Složení směsi ve velké vzdálenosti je jistě ovlivněno mnoha "nejadernými" faktory jako jsou meteorologické vlivy,
velikost aerosolů, fyzikálně-chemické vlastnosti radionuklidů atd.
Nechť factual(x;t1) představuje četnost (hustotu) rozpadových konstant x, která popisuje skutečné složení
ve velké vzdálenosti v čase t1 (podíl radionuklidu s rozpadovou konstantou x jehož množství je Co(xi)).
Parametr t1 odpovídá době od okamžiku nehody/výbuchu do okamžiku spadu (počátku měření)
(například t1 = 5.5 dnů pro 1 květen 1986).
Funkce factual(x; t1) je ovlivněna mnoha faktory, z nichž jeden je dominantní a je to právě radioaktivní rozpad.
Tento faktor lze snadno oddělit od ostatních v případě, že je stáří směsi radionuklidů známé.
Například doba života 137Cs je asi 11 000 dnů, zatímco doba života 131I je asi 8 dnů.
Množství 131I je ve směsi tedy více ovlivněno radioaktivním rozpadem v čase t1.
Vliv radioaktivního rozpadu na funkci factual lze eliminovat, pokud je skutečná četnost nahrazena virtuální četností v čase t=0
(jakési fiktivní zastoupení pokud by se atomy radioaktivně nerozpadaly).
Tuto virtualní četnost fv(x) lze definovat takto: fv(x) = factual(x; t1) exp(+t1x)
Funkce fv(x) je virtuální, neboť se liší od skutečného složení v čase t=0.
fv(x) je výsledkem všech ostatní faktorů ovlivňujících složení směsi ve velké vzdálenosti.
Tato funkce vyjadřuje skutečnost, že různé radionuklidy mají různou pravděpodobnost dosažení cíle spadu od místa výbuchu
(například vzácné plyny obsažené v inventáři reaktoru maji zcela jinou šanci dosáhnout vzdálené lokality, než například těžké kovy).
Celková radioaktivita je tedy v čase t (který je počítán od okamžiku výbuchu/nehody) součtem jednotlivých aktivit
xfv(x)exp(-xt) a může být použita následující rovnice:
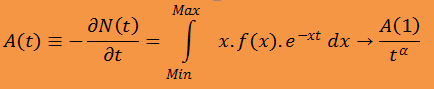
, kde N(t) je počet všech radioaktivních atomů v čase t, alfa >0 pro t > t1,
Min a Max představují minimální a maximální rozpadovou konstantu ve směsi v okamžiku spadu (resp. v okamžiku počátku měření).
Pokud položíme xmin = 0 a xmax = nekonečno, potom je A(t) Laplaceovou transformací součinu xfv(x).
Tento matematický formalismus je identický s formalismem popisujícím pokles postnatální úmrtnosti,
tedy s teorií vrozených individuálních rizik.
Celková aktivita směsi štěpných produktů a postnatální úmrtnost v heterogenní populaci mohou být popsány stejnou rovnicí.
Tento formalismus umí vysvětlit lineární pokles v log-log měřítku a umožňuje výpočet směrnice poklesu v log-log měřítku.
Vrozené individuální riziko v lidské populaci tedy odpovídá rozpadové konstantě radionuklidu ve směsi štěpných produktů.
Podle této teorie směrnice závisí pouze na typu statistického rozdělení a překvapivě nezávisí na konkrétních hodnotách
parametrů statistického rozdělení (v širokém rozmezí těchto hodnot).
Pro lognormální rozdělení nebo pokud lze nahradit hustotu f(x) funkcí const./x,
je směrnice rovna -1.
Teoretická hodnota směrnice je -2 pokud je f(x) hustota normálního rozdělení s velkým rozptylem,
případně pokud jde o hustotu rovnoměrného rozdělení.
Obecně platí:
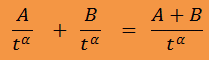
Pokud je směrnice poklesu ve dvou částech celkového zdroje aktivity stejná, potom je stejná i v celku (což neplatí pro exponenciální pokles, který není v tomto smyslu aditivní).
Z tohoto důvodu lze podmínky konvergence integrálu k nepřímé úměře výrazně zobecnit.
Zdroje aktivity mohou být rozděleny na dílčí zdroje. Dostačující podmínkou je, aby rozpadové konstanty byly přibližně
log-normálně rozděleny nebo aby pro četnost rozpadových konstant v každém zdroji platilo f(x)=const./x.
Celková aktivita ve velké vzdálenosti od zdroje je nepřímoúměrná času pokud je okamžik výbuchu použit jako počátek časové osy.
Model se směrnicí 1,2 je příliš optimistický a nepopisuje skutečná data.
Odhad dávky je jednoduchý pokud vztah mezi časem a dávkovým příkonem obsahuje dva parametry (lineární pokles v log-log měřítku).
Pokud je směrnice poklesu známa dopředu lze dávku odhadnout z jednoho měření dávkového příkonu.
Současně musí být znám okamžik výbuchu či nehody. Toto bylo splněno také v případě vzorku spadu z Bratislavy z roku 1965.
Směrnice je rovna -1 i v tomto případě. Tuto skutečnost lze vysvětlit jako důsledek lognormálního rozdělení
rozpadových konstant.
English